Three State Dynamic Wake

Accurate wake models are critical for predicting helicopter performance and handling qualities. For starters, accurate prediction of the average induced velocity over the rotor disk is required to predict induced drag and therefore torque, power and engine requirements. In many cases, we also need to know how this flow is distributed over the rotor. For example, the wake is typically more concentrated in the aft portion of the disk in forward flight. This nonuniformity of the wake impacts flapping and helicopter response. In this article we discuss so-called three state dynamic wake models which are simple yet useful for performance and handling quality predictions. (Abbreviations and symbols used here and throughout this site are defined here.)

The three state variables are denoted by \(\lambda = (\lambda_0, \lambda_s, \lambda_c)\). The induced velocity \(v_i\) at a blade section at a distance \(r\) from the hub at an azimuth \(\Psi\) is \begin{equation} v_i(r,\Psi )=\lambda_0 + r\lambda_s \sin \Psi + r\lambda_c \cos \Psi \label{eq:tsvi} . \end{equation}

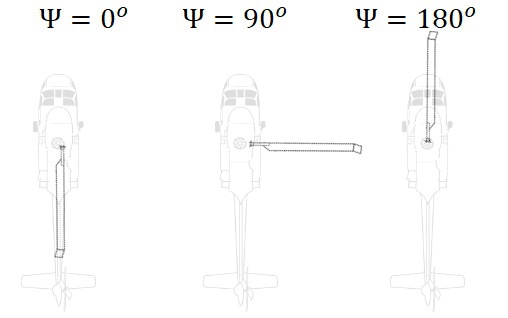
Here \(\Psi=0\) represents a blade over the tail of the helicopter, \(\Psi=90^o\) represents a blade on the right side of the helicopter, \(\Psi=180^o\) over the nose, .... As you can see, \(\lambda_0\) represents the mean inflow at the rotor, while \(\lambda_s,\lambda_c\) are 1/rev oscillatory components. Increasing \(\lambda_0\) primarily decreases rotor thrust, while \(\lambda_s\) and \(\lambda_c\) primarily impact longitudinal and lateral flapping, respectively. (To understand why \(\lambda_s\), which causes a wake differential on the right/left sides of the rotor, impacts fore/aft flapping, see this article on flap dynamics.)

What’s left is to explain how to compute the state variables \(\lambda\). This is typically presented in state-space representation with the matrix equation $$ \begin{equation} M\dot{\lambda} + K\lambda = C. \label{eq:ssrep} \end{equation}$$ In other words, a linear, first order differential equation is used to compute the \(\lambda\). With help from a computer, we solve for the time derivative \(\dot{\lambda}\), which is a function of \(\lambda\) and other time-varying values. We then integrate \(\dot{\lambda}\) to get the \(\lambda\) used in the rotor analysis.

Pitt and Peters originally proposed this wake model and specified the matrices \(M, K\) and \(C\) as defined below. While those are good values, other versions of \(M\) and \(K\) have subsequently been found useful in certain applications. The point here being that \(M\) and \(K\) may be empirically or otherwise chosen for a desired scenario. \(C\) is almost always the thrust, roll and pitch coefficients.

$$ \begin{equation} C = \begin{bmatrix} C_T & C_L & C_M \end{bmatrix}^T \end{equation} $$

$$ \begin{equation} M = \begin{bmatrix} \frac{128}{75\pi} & 0 & 0 \\ 0 & \frac{16}{45\pi} & 0 \\ 0 & 0 & \frac{16}{45\pi} \end{bmatrix} \end{equation} $$

$$ \begin{equation} K = \begin{bmatrix} V_m & 0 & 0 \\ 0 & V & 0 \\ 0 & 0 & V \end{bmatrix} \begin{bmatrix} .5 & 0 & -\frac{15\pi X}{64} \\ 0 & 2(1+X^2) & 0 \\ \frac{15\pi X}{64} & 0 & 2(1-X^2) \end{bmatrix}^{-1} \end{equation} $$

Where \(V_m = \sqrt{\mu^2+\lambda^2}\), \(V=\frac{\mu^2+\lambda(\lambda+\nu)}{V_m}\) and \(X=\tan \frac{\chi}{2} \).

Limitations

Three state wake models are useful due to their simplicity, computational efficiency and ability to predict steady and 1/rev wake effects. However, they are not suitable for predicting off-axes responses to control inputs, vortex ring state, or ground effect.

Similar Models and References

The original paper from Pitt and Peters is here. The Pitt-Peters model was generalized to handle a finite number of states by Peters and He. The model was improved to be based on a velocity potential rather than an acceleration potential by Morillo and Peters. Hoydonck wrote an excellent review of rotorcraft wake models in “A Review of Rotorcraft Wake Modeling Methods for Flight Dynamics Applications.” Wayne Johnson provides derivations for dynamic, 1/rev wake models (and many other aspects of rotorcraft) in his famous book “Helicopter Theory.”